Notes: Introduction to Nonparametric Bootstrapping

Ivan Jacob Agaloos Pesigan

2020-07-16

Source: vignettes/notes/notes_intro_nb.Rmd 
library(jeksterslabRboot)

Random Variable

Let \(X\) be a random variable from a normal distribution with \(\mu = 100\) and \(\sigma^2 = 225\).

\[\begin{equation} X \sim \mathcal{N} \left( \mu = 100, \sigma^2 = 225 \right) (\#eq:dist-norm-X-r) \end{equation}\]

This data generating function is referred to as \(F\).

Population Parameters
Variable Description Notation Value
mu Population mean. \(\mu\) 100
sigma2 Population variance. \(\sigma^2\) 225
sigma Population standard deviation. \(\sigma\) 15

For a sample size of \(n = 1000\), if the parameter of interest \(\theta\) is the mean \(\mu\), using the know parameters, the variance of the sampling distribution of the mean is

\[\begin{equation} \mathrm{Var} \left( \hat{\mu} \right) = \frac{ \sigma^2 } { n } = 0.225 \end{equation}\]

and the standard error of the mean is

\[\begin{equation} \mathrm{se} \left( \hat{\mu} \right) = \frac{ \sigma } { \sqrt{n} } = 0.4743416 \end{equation}\]

Sampling Distribution of \(\hat{\theta}\) with Known Parameters
Variable Description Notation Value
n Sample size. \(n\) 1000.0000000
theta Population mean. \(\theta = \mu\) 100.0000000
var_thetahat Variance of the sampling distribution of the mean. \(\mathrm{Var} \left( \hat{\theta} \right) = \frac{ \sigma^2 }{n}\) 0.2250000
se_thetahat Standard error of the mean. \(\mathrm{se} \left( \hat{\theta} \right) = \frac{ \sigma }{\sqrt{n}}\) 0.4743416

Sample Data

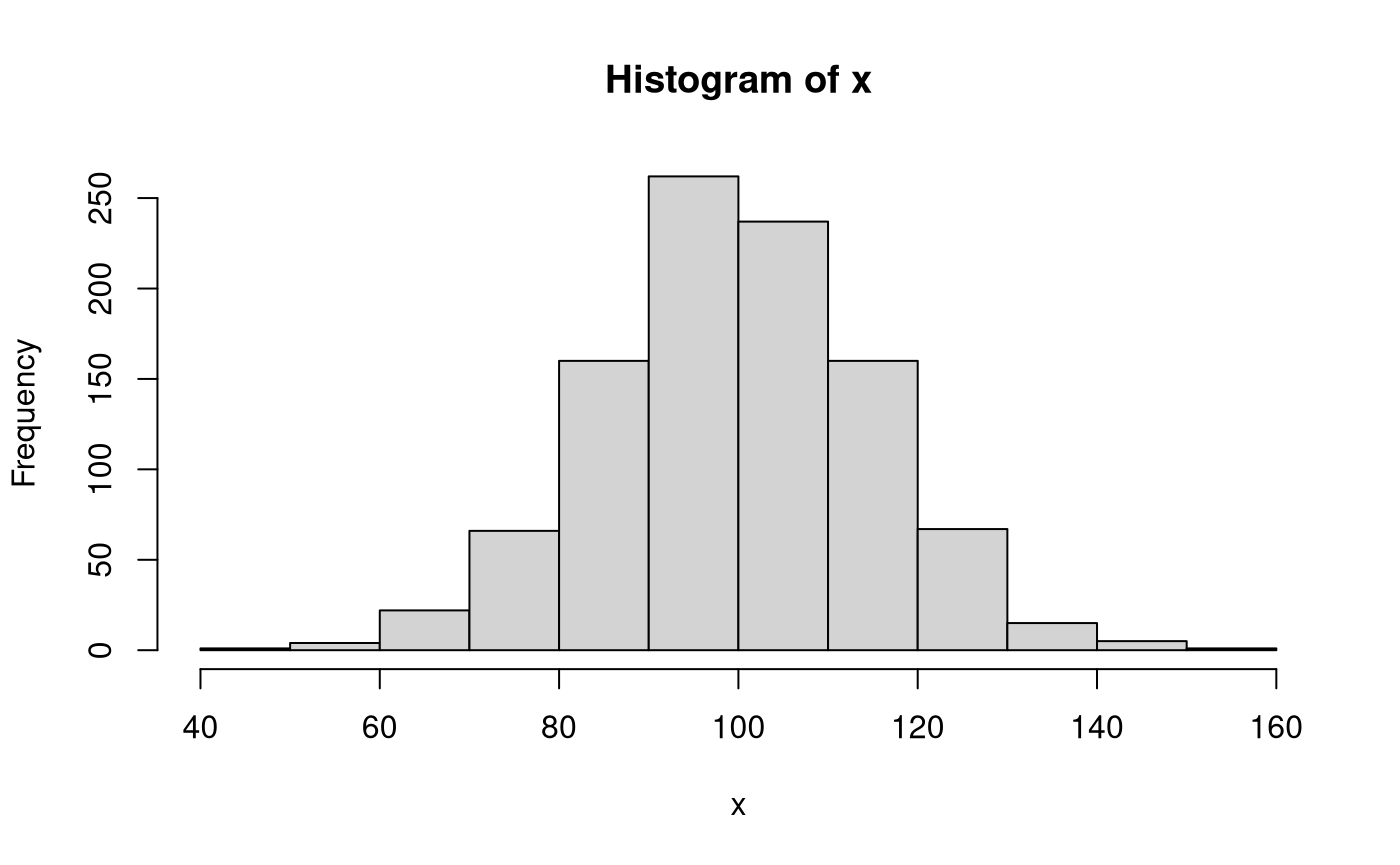
Let \(\mathbf{x}\) be a vector of length \(n = 1000\) of realizations of the random variable \(X\). Each observation \(i\) is independently sampled from the normal distribution with \(\mu = 100\) and \(\sigma^2 = 225\).

\[\begin{equation} x = X \left( \omega \right) (\#eq:dist-random-variable-1) \end{equation}\]

\[\begin{equation} \mathbf{x} = \begin{bmatrix} x_1 = X \left( \omega_1 \right) \\ x_2 = X \left( \omega_2 \right) \\ x_3 = X \left( \omega_3 \right) \\ x_i = X \left( \omega_i \right) \\ \vdots \\ x_n = X \left( \omega_n \right) \end{bmatrix}, \\ i = \left\{ 1, 2, 3, \dots, n \right\} (\#eq:dist-random-variable-2) \end{equation}\]

This is accommplished in R using the rnorm() function with the following arguments n = 1000, mean = 100, and sd = 15. rnorm() returns a vector of length n.

x <- rnorm(
  n = n,
  mean = mu,
  sd = sigma
)
str(x)
#>  num [1:1000] 120.6 91.5 105.4 109.5 106.1 ...

We can calculate sample statistics using the sample data \(\mathbf{x}\). Note that a hat (^) indicates that the quantity is an estimate of the parameter using sample data.

Sample Statistics (Parameter Estimates)
Variable Description Notation Value
n Sample size. \(n\) 1000.0000000
thetahat Sample mean. \(\hat{\theta} = \hat{\mu} = \frac{1}{n} \sum_{i = 1}^{n} x_i\) 99.6126336
sigma2hat Sample variance. \(\hat{\sigma}^2 = \frac{1}{n - 1} \sum_{i = 1}^{n} \left( x_i - \hat{\mu} \right)^2\) 226.1359868
sigmahat Sample standard deviation. \(\hat{\sigma} = \sqrt{\frac{1}{n - 1} \sum_{i = 1}^{n} \left( x_i - \hat{\mu} \right)^2}\) 15.0378186
varhat Estimate of the variance of the sampling distribution of the mean. \(\widehat{\mathrm{Var}} \left( \hat{\theta} \right) = \frac{ \hat{\sigma}^2 }{n}\) 0.2261360
sehat Estimate of the standard error of the mean. \(\widehat{\mathrm{se}} \left( \hat{\theta} \right) = \frac{ \hat{\sigma} }{\sqrt{n}}\) 0.4755376

Nonparametric Bootstrapping

\(\mathbf{x}\) which is a vector of realizations of the random variable \(X\) is used in bootstrapping. This sample data is referred to as the empirical distribution \(\hat{F}\).

In nonparametric bootstrapping, the empirical distribution \(\hat{F}\) is resampled \(B\) number of times (1000 in the current example) with replacement.

Bootstrap Samples

\(\mathbf{x}^{*}\) is a set of \(B\) bootstrap samples.

\[\begin{equation} \mathbf{x}^{*} = \begin{bmatrix} \mathbf{x}^{*1} = \left\{ x^{*1}_{1}, x^{*1}_{2}, x^{*1}_{3}, x^{*1}_{i}, \dots, x^{*1}_{n} \right\} \\ \mathbf{x}^{*2} = \left\{ x^{*2}_{1}, x^{*2}_{2}, x^{*2}_{3}, x^{*2}_{i}, \dots, x^{*2}_{n} \right\} \\ \mathbf{x}^{*3} = \left\{ x^{*3}_{1}, x^{*3}_{2}, x^{*3}_{3}, x^{*3}_{i}, \dots, x^{*3}_{n} \right\} \\ \mathbf{x}^{*b} = \left\{ x^{*b}_{1}, x^{*b}_{2}, x^{*b}_{3}, x^{*b}_{i}, \dots, x^{*b}_{n} \right\} \\ \vdots \\ \mathbf{x}^{*B} = \left\{ x^{*B}_{1}, x^{*B}_{2}, x^{*B}_{3}, x^{*B}_{i}, \dots, x^{*B}_{n} \right\} \end{bmatrix}, \\ b = \left\{ 1, 2, 3, \dots, B \right\}, \\ i = \left\{ 1, 2, 3, \dots, n \right\} \end{equation}\]

The function nb() from the jeksterslabRboot package can be used to generate B nonparametric bootstrap samples. The argument data takes in a vector, matrix, or data frame. data is the empirical distribution \(\hat{F}\). In the example below, we use x, which is the sample data above, as the argument data. The argument B takes an integer. B is the number of bootstrap samples B = 1000 in our case. Optional arguments include par which is a logical argument to enable the use of multiple cores and ncores which is the number of cores to use. The nb() function returns a list of length B bootstrap samples. \(x^{*}\) is saved as xstar.

xstar <- nb(
  data = x,
  B = B
)
str(xstar, list.len = 6)
#> List of 1000
#>  $ : num [1:1000] 128.4 119.5 115.2 75.8 116.4 ...
#>  $ : num [1:1000] 110.9 94.6 113.5 98.4 78 ...
#>  $ : num [1:1000] 121.7 81.9 89.1 90.8 82.2 ...
#>  $ : num [1:1000] 96.7 55.1 102.4 89.1 104.1 ...
#>  $ : num [1:1000] 110 84.5 84.2 105.6 88.8 ...
#>  $ : num [1:1000] 92.5 83.3 95.9 100.7 96.1 ...
#>   [list output truncated]

Bootstrap Sampling Distribution

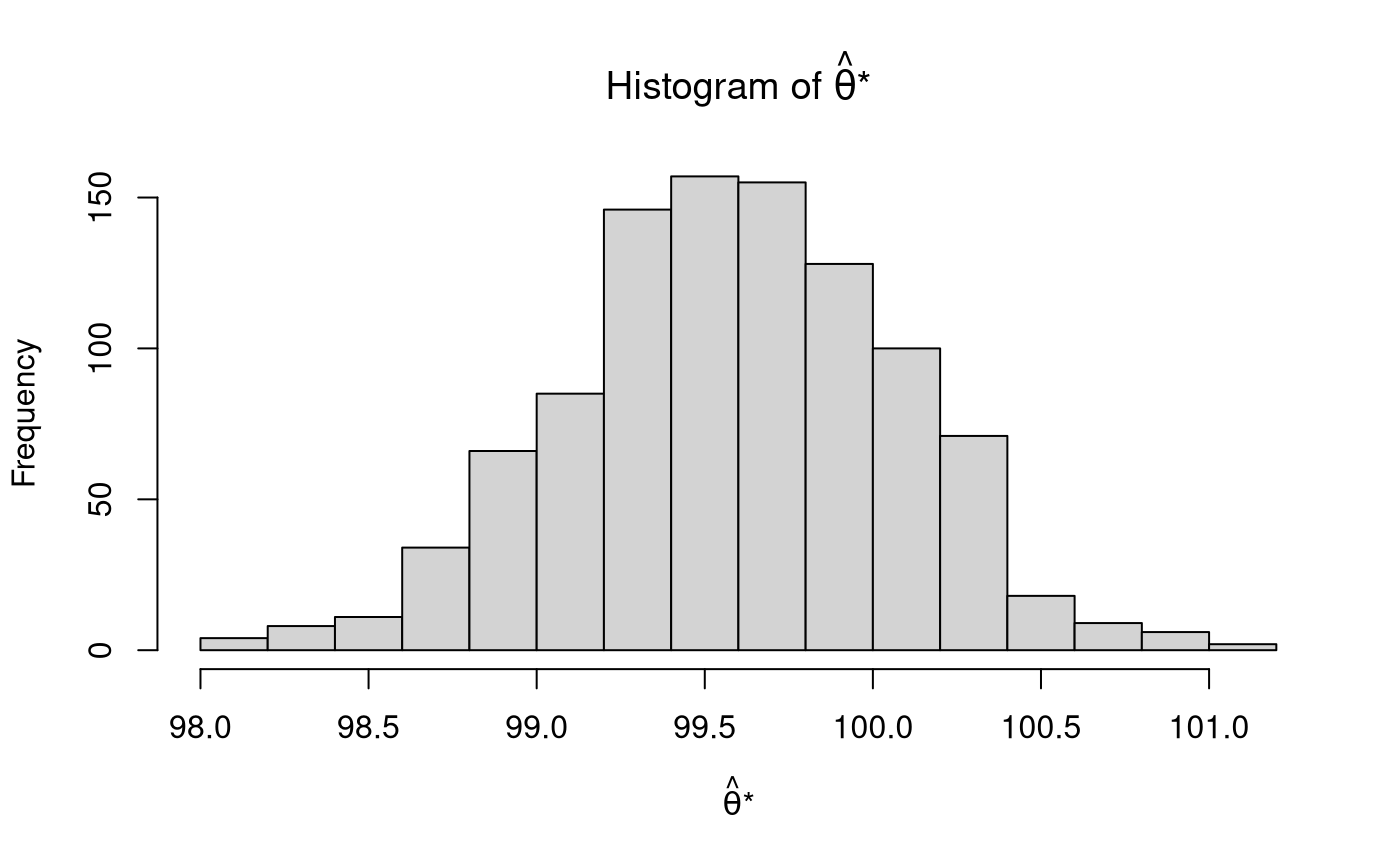
The parameter is estimated for each of the \(B\) bootstrap samples. For example, if we are interested in making inferences about the mean, we calculate the sample statistic (\(\mathrm{s}\)), that is, the sample mean, for each element of \(\mathbf{x}^{*}\). The \(B\) estimated parameters form the bootstrap sampling distribution \(\boldsymbol{\hat{\theta}^{*}}\).

\[\begin{equation} \boldsymbol{\hat{\theta}^{*}} = \begin{bmatrix} \hat{\theta}^{*} \left( 1 \right) = \mathrm{s} \left( \mathbf{x}^{*1} \right) \\ \hat{\theta}^{*} \left( 2 \right) = \mathrm{s} \left( \mathbf{x}^{*2} \right) \\ \hat{\theta}^{*} \left( 3 \right) = \mathrm{s} \left( \mathbf{x}^{*3} \right) \\ \hat{\theta}^{*} \left( b \right) = \mathrm{s} \left( \mathbf{x}^{*b} \right) \\ \vdots \\ \hat{\theta}^{*} \left( B \right) = \mathrm{s} \left( \mathbf{x}^{*B} \right) \end{bmatrix}, \\ b = \left\{ 1, 2, 3, \dots, B \right\} \end{equation}\]

sapply is a useful tool in R to apply a function to each element of a list. In our case, we apply the function mean() to each element of the list xstar. sapply simplifies the output when possible. In our case, sapply returns a vector, thetahatstar. The *apply functions as well as their parallel counterparts (e.g., parSapply) can be used to simplify repetitive tasks.

thetahatstar <- sapply(
  X = xstar,
  FUN = mean
)
str(thetahatstar)
#>  num [1:1000] 100.5 99.5 99.4 99.8 100 ...

Estimated Bootstrap Standard Error

The estimated bootstrap standard error is given by

\[\begin{equation} \widehat{\mathrm{se}}_{\mathrm{B}} \left( \hat{\theta} \right) = \sqrt{ \frac{1}{B - 1} \sum_{b = 1}^{B} \left[ \hat{\theta}^{*} \left( b \right) - \hat{\theta}^{*} \left( \cdot \right) \right]^2 } = 0.4879561 \end{equation}\]

where

\[\begin{equation} \hat{\theta}^{*} \left( \cdot \right) = \frac{1}{B} \sum_{b = 1}^{B} \hat{\theta}^{*} \left( b \right) = 99.5814296 . \end{equation}\]

Note that \(\widehat{\mathrm{se}}_{\mathrm{B}} \left( \hat{\theta} \right)\) is the standard deviation of \(\boldsymbol{\hat{\theta}^{*}}\) and \(\hat{\theta}^{*} \left( \cdot \right)\) is the mean of \(\boldsymbol{\hat{\theta}^{*}}\) .

Nonparametric Bootstrapping Results
Variable Description Notation Value
B Number of bootstrap samples. \(B\) 1000.0000000
mean_thetahatstar Mean of \(B\) sample means. \(\hat{\theta}^{*} \left( \cdot \right) = \frac{1}{B} \sum_{b = 1}^{B} \hat{\theta}^{*} \left( b \right)\) 99.5814296
var_thetahatstar Variance of \(B\) sample means. \(\widehat{\mathrm{Var}}_{\mathrm{B}} \left( \hat{\theta} \right) = \frac{1}{B - 1} \sum_{b = 1}^{B} \left[ \hat{\theta}^{*} \left( b \right) - \hat{\theta}^{*} \left( \cdot \right) \right]^2\) 0.2381012
sd_thetahatstar Standard deviation of \(B\) sample means. \(\widehat{\mathrm{se}}_{\mathrm{B}} \left( \hat{\theta} \right) = \sqrt{ \frac{1}{B - 1} \sum_{b = 1}^{B} \left[ \hat{\theta}^{*} \left( b \right) - \hat{\theta}^{*} \left( \cdot \right) \right]^2 }\) 0.4879561

Confidence Intervals

Confidence intervals can be constructed around \(\hat{\theta}\) . The functions pc(), bc(), and bca() from the jeksterslabRboot package can be used to construct confidence intervals using the default alphas of 0.001, 0.01, and 0.05. Wald confidence intervals (wald()) are added for comparison. The confidence intervals can also be evaluated. Since we know the population parameter theta \(\left(\theta = \mu = 100 \right)\), we can check if our confidence intervals contain the population parameter.

See documentation for wald(), pc(), bc(), and bca() from the jeksterslabRboot package on how confidence intervals are constructed.

See documentation for zero_hit(), theta_hit(), len(), and shape() from the jeksterslabRboot package on how confidence intervals are evaluated.

wald_out <- wald(
  thetahat = thetahat,
  sehat = sehat,
  eval = TRUE,
  theta = theta
)
wald_out_t <- wald(
  thetahat = thetahat,
  sehat = sehat,
  dist = "t",
  df = df,
  eval = TRUE,
  theta = theta
)
pc_out <- pc(
  thetahatstar = thetahatstar,
  thetahat = thetahat,
  wald = TRUE,
  eval = TRUE,
  theta = theta
)
bc_out <- bc(
  thetahatstar = thetahatstar,
  thetahat = thetahat,
  wald = TRUE,
  eval = TRUE,
  theta = theta
)
bca_out <- bca(
  thetahatstar = thetahatstar,
  thetahat = thetahat,
  data = x,
  fitFUN = mean,
  wald = TRUE,
  eval = TRUE,
  theta = theta
)
Confidence Intervals
statistic p se ci_0.05 ci_0.5 ci_2.5 ci_97.5 ci_99.5 ci_99.95 zero_hit_0.001 zero_hit_0.01 zero_hit_0.05 theta_hit_0.001 theta_hit_0.01 theta_hit_0.05 length_0.001 length_0.01 length_0.05 shape_0.001 shape_0.01 shape_0.05
wald 209.4737 0 0.4755376 98.04786 98.38773 98.68060 100.5447 100.8375 101.1774 0 0 0 1 1 1 3.129538 2.449807 1.864073 1.0000000 1.0000000 1.0000000
wald_t 209.4737 0 0.4755376 98.04322 98.38539 98.67947 100.5458 100.8399 101.1820 0 0 0 1 1 1 3.138826 2.454496 1.866334 1.0000000 1.0000000 1.0000000
pc 204.1426 0 0.4879561 98.06326 98.21239 98.63318 100.4538 100.8186 101.0342 0 0 0 1 1 1 2.970926 2.606214 1.820627 0.9175043 0.8612579 0.8588161
bc 204.1426 0 0.4879561 98.06337 98.28194 98.68233 100.5633 100.8607 101.0384 0 0 0 1 1 1 2.974997 2.578771 1.880929 0.9202657 0.9379197 1.0218532
bca 204.1426 0 0.4879561 98.06337 98.28193 98.68232 100.5632 100.8607 101.0384 0 0 0 1 1 1 2.974991 2.578771 1.880891 0.9202613 0.9379057 1.0217909

Notes

The estimated bootstrap standard error is similar to results from the closed form solution. The estimated bootstrap confidence intervals are also close to the Wald confidence intervals. While a closed form solution for the standard error is available in this simple example, bootstrap standard errors and confidence intervals can be used in situations when standard errors are not easy to calculate.

References