Studentized Residuals

Calculates studentized residuals using $$ t_i = \frac{\hat{\varepsilon}_{i}}{\hat{\sigma}_{\varepsilon}^{2} \sqrt{1 - h_{ii}}} $$

tepsilonhat(X, y)

Arguments

X	n by k numeric matrix. The data matrix \(\mathbf{X}\) (also known as design matrix, model matrix or regressor matrix) is an \(n \times k\) matrix of \(n\) observations of \(k\) regressors, which includes a regressor whose value is 1 for each observation on the first column.
y	Numeric vector of length n or n by 1 matrix. The vector \(\mathbf{y}\) is an \(n \times 1\) vector of observations on the regressand variable.

Value

Returns studentized residuals.

See also

Other residuals functions: .My(), .tepsilonhat(), .yminusyhat(), My(), epsilonhat(), yminusyhat()

Author

Ivan Jacob Agaloos Pesigan

Examples

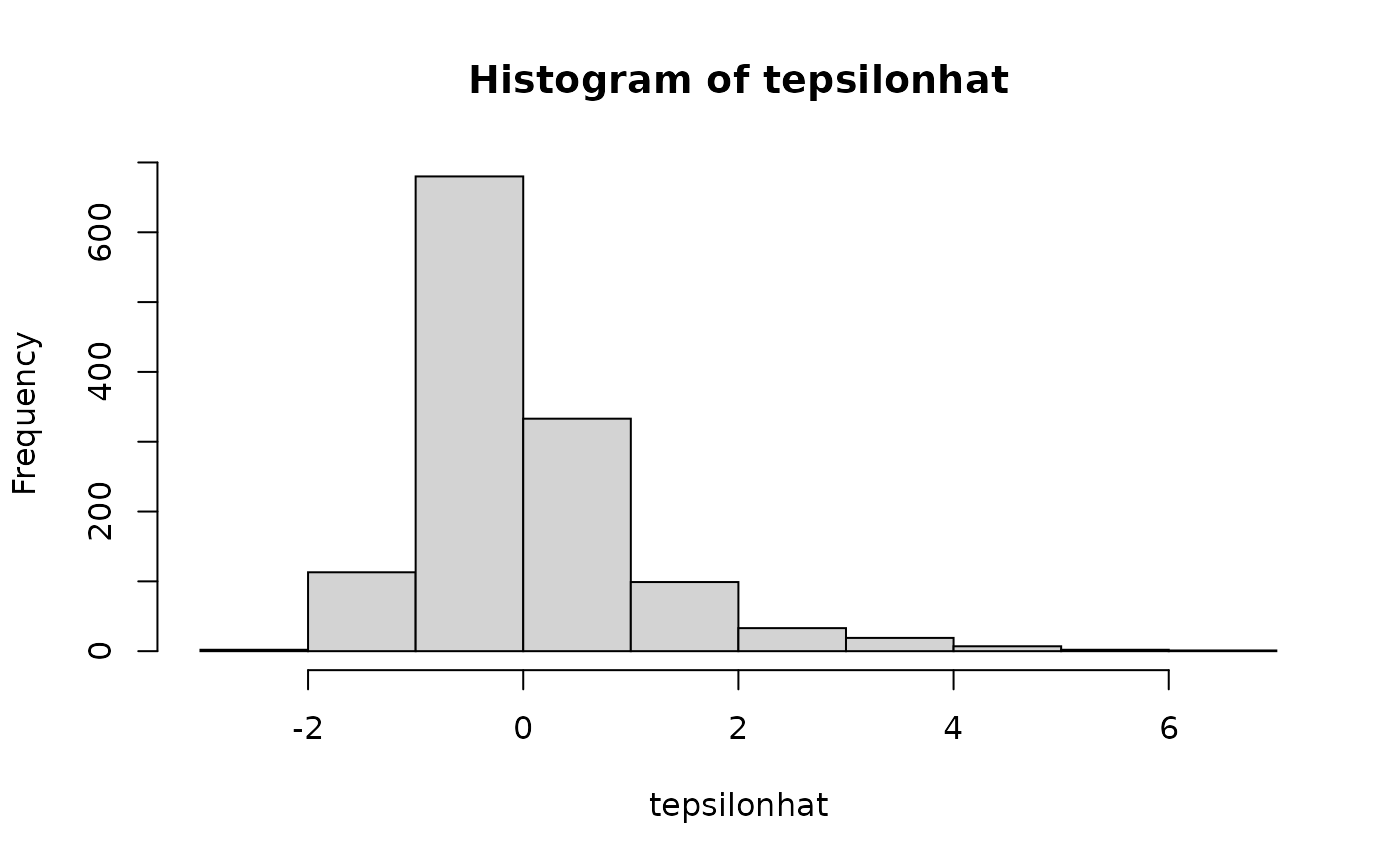
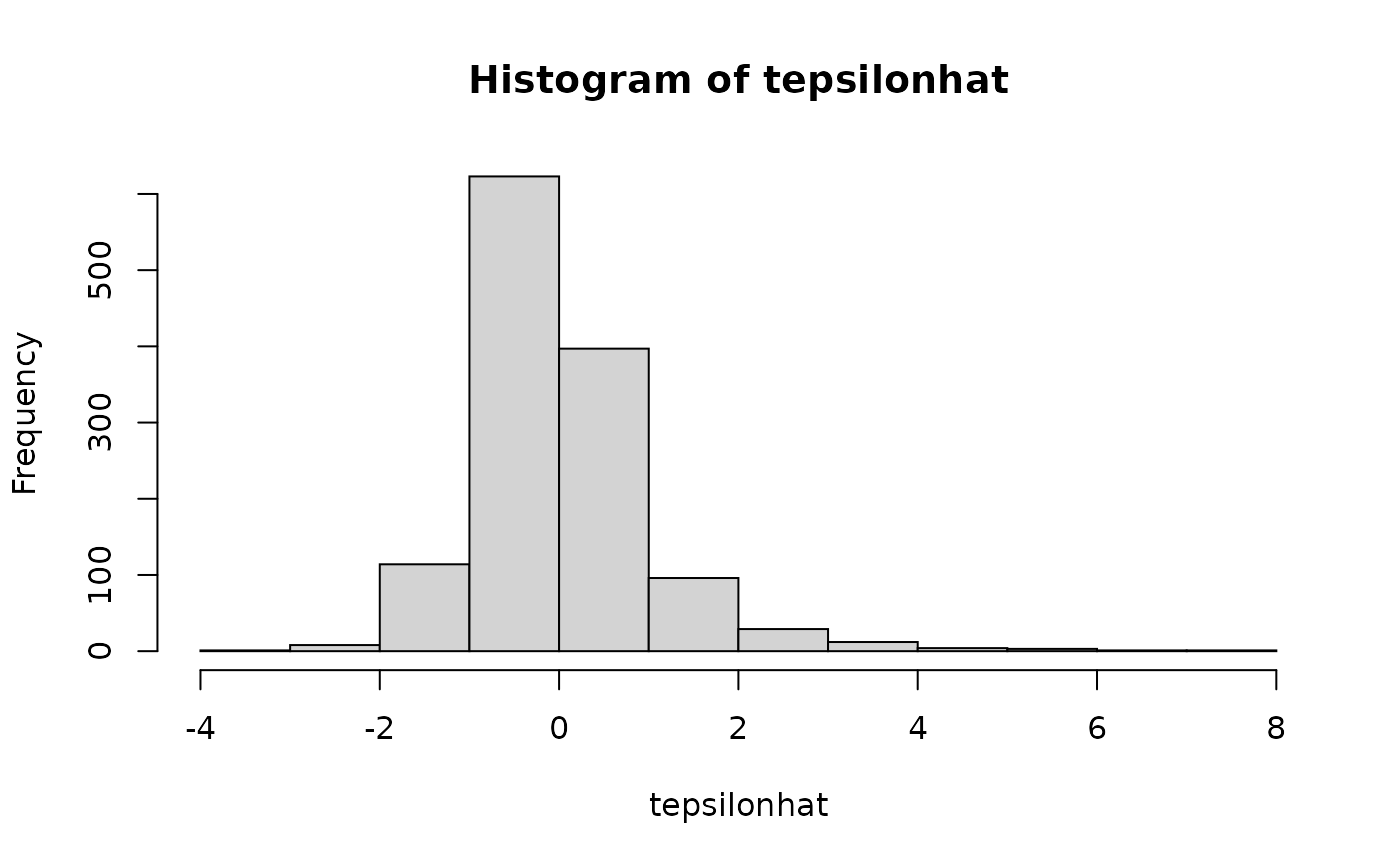
# Simple regression------------------------------------------------
X <- jeksterslabRdatarepo::wages.matrix[["X"]]
X <- X[, c(1, ncol(X))]
y <- jeksterslabRdatarepo::wages.matrix[["y"]]
tepsilonhat <- tepsilonhat(X = X, y = y)
hist(tepsilonhat)

# Multiple regression----------------------------------------------
X <- jeksterslabRdatarepo::wages.matrix[["X"]]
# age is removed
X <- X[, -ncol(X)]
tepsilonhat <- tepsilonhat(X = X, y = y)
hist(tepsilonhat)